DSA-8：列表及其接口设计2

列表的基本接口（其二）

插入

列表的插入操作有以下四种形式：

• 将元素作为首节点插入
• 将元素作为末节点插入
• 将元素作为某节点的后继插入
• 将元素作为某节点的前驱插入

上述操作都可以使用列表节点对象的前插入或后插入方法实现。**注意，在插入元素后不要忘了更新列表的规模_size**。

前插入

列表的前插入是将某个元素作为某节点的前驱插入列表的过程，其代码如下：

template <typename T> //将e紧靠当前节点之前插入于当前节点所属列表（设有哨兵头节点header）
ListNodePosi<T> ListNode<T>::insertAsPred ( T const& e ) {
   ListNodePosi<T> x = new ListNode ( e, pred, this ); //创建新节点
   pred->succ = x; pred = x; //设置正向链接
   return x; //返回新节点的位置
}

上述代码第3行中ListNode构造函数中的参数this指代的是当前节点。

该算法首先创建了一个新的节点new，并且ListNode的构造函数将其内容设为e，将新节点new的后继的succ指针指向当前节点this，令新节点new的pred指针指向当前节点this的前驱节点。然后，需要将当前节点this的前驱的succ指针指向新节点new，将当前节点this的pred指针指向新节点new。注意，代码第4行中调整前驱和后继指针的顺序不可以颠倒，否则会使新节点的succ指针指向它本身。

前插入的算法可以用下图表示：

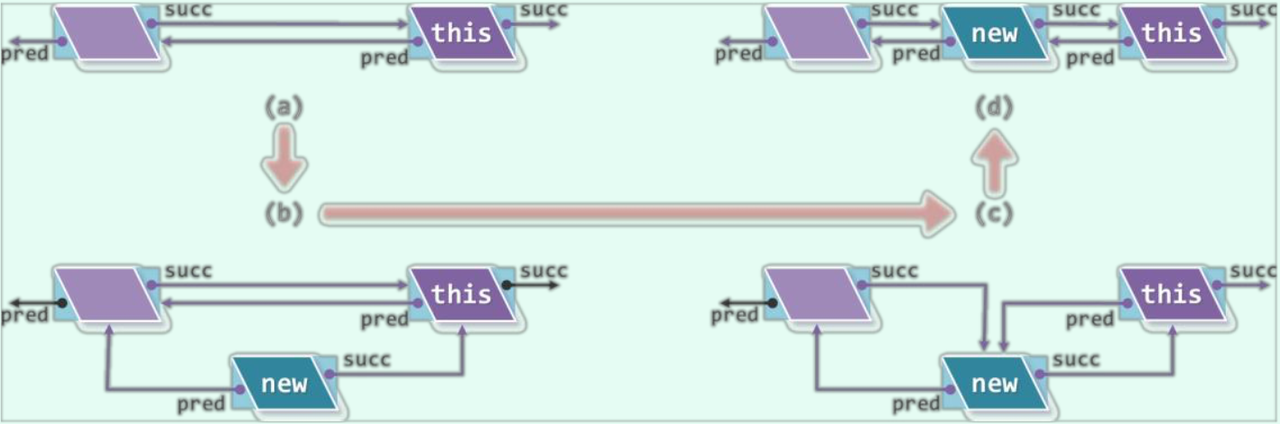
如果需要将元素作为某节点的前驱插入，只需要调用该节点的前插入成员函数insertAsPred()即可。如果需要将元素作为列表的首节点插入，同样只需要调用列表头哨兵中的前插入函数即可。

后插入

后插入的操作过程与最终效果同前插入完全对称，这里仅给出算法的代码，不再过多解释。

template <typename T> //将e紧随当前节点之后插入于当前节点所属列表（设有哨兵尾节点trailer）
ListNodePosi<T> ListNode<T>::insertAsSucc ( T const& e ) {
   ListNodePosi<T> x = new ListNode ( e, this, succ ); //创建新节点
   succ->pred = x; succ = x; //设置逆向链接
   return x; //返回新节点的位置
}

上述插入的操作过程都可以在常数时间内完成。

基于复制的构造函数

对列表各种不同的复制操作都可以使用”复制列表中自位置p起的n个节点“的底层操作实现。该底层操作首先要对新构造出来的列表创建其头、尾哨兵节点并做初始化，然后再将待复制列表自p起的n个节点都作为末节点插入到新列表中即可。该底层算法的总体运行时间为$\mathcal O(\rm n + 1)$。

使用上面给出的底层算法，可以实现下面的构造操作：

• 复制列表中自位置p起的n个元素
• 整体复制列表
• 复制列表中自第r项元素起的n个元素

注意上面的最后一个操作，首先其需要花费$\mathcal O(\rm r +1)$的时间找到r的位置，然后再花$\mathcal O (\rm n)$的时间进行复制，因此器总体时间复杂度为$\mathcal O (\rm r+n+1)$。

删除

删除列表中指定节点p的算法如下：

template <typename T> T List<T>::remove ( ListNodePosi<T> p ) { //删除合法节点p，返回其数值
   T e = p->data; //备份待删除节点的数值（假定T类型可直接赋值）
   p->pred->succ = p->succ; p->succ->pred = p->pred; //后继、前驱
   delete p; _size--; //释放节点，更新规模
   return e; //返回备份的数值
}

在删除节点之前，首先要令被删除节点的前驱和后继相互链接，然后将孤立出来的节点删除，最后再更新列表的规模。

该算法可以在常数时间内完成。

析构

列表在析构时，需要清空列表中的各个节点，然后再释放头、尾哨兵节点。可以通过“反复调用删除首节点（header -> suuc），直到列表规模变为0”的方法实现对列表中各个节点的清除。析构方法的运行时间为$\mathcal O (\rm n)$，线性正比于列表原先的规模。

唯一化

列表的唯一化算法与向量的类似。代码如下：

template <typename T> int List<T>::deduplicate() {
   int oldSize = _size; ListNodePosi<T> p = first();
   for ( Rank r = 0; p != trailer; p = p->succ ) //O(n)
      if ( ListNodePosi<T> q = find(p->data, r, p) )
         remove(q); //此时q与p雷同，但删除前者更为简明
      else r++; //r为无重前缀的长度
   return oldSize - _size; //删除元素总数
}

该算法总共需要进行$\rm n$步迭代，每一步迭代中find()操作所需要的时间线性正比于查找区间的宽度，节点每次的remove()操作仅需要线性时间，因此总体执行时间应该为：$1 + 2 + 3 + … + \rm{n} = \mathcal O(\rm n^2) $。

遍历

列表的遍历接口也与向量相似，其实现如下：

template <typename T> void List<T>::traverse ( void ( *visit ) ( T& ) ) //借助函数指针机制遍历
{  for ( ListNodePosi<T> p = header->succ; p != trailer; p = p->succ ) visit ( p->data );  }

template <typename T> template <typename VST> //元素类型、操作器
void List<T>::traverse ( VST& visit ) //借助函数对象机制遍历
{  for ( ListNodePosi<T> p = header->succ; p != trailer; p = p->succ ) visit ( p->data );  }

有序列表的基本接口

若列表中所有节点的逻辑次序与其大小次序完全一致，则称作有序列表。这里约定采用非降次序，并且假设列表中的元素类型T直接支持大小比较，或已重载相关操作符。

唯一化

在有序列表中，雷同的节点也必然在逻辑上彼此紧邻。因此可以实现重复节点删除算法：

template <typename T> int List<T>::uniquify() { //成批剔除重复元素，效率更高
   if ( _size < 2 ) return 0; //平凡列表自然无重复
   int oldSize = _size; //记录原规模
   ListNodePosi<T> p = first(); ListNodePosi<T> q; //p为各区段起点，q为其后继
   while ( trailer != ( q = p->succ ) ) //反复考查紧邻的节点对(p, q)
      if ( p->data != q->data ) p = q; //若互异，则转向下一区段
      else remove ( q ); //否则（雷同），删除后者
   return oldSize - _size; //列表规模变化量，即被删除元素总数
}

算法中，位置指针p和q分别指向每一对相邻的节点，若两者雷同则删除q，否则指向下一对相邻节点。

该算法的运行时间为$\mathcal O(\rm _size) = \mathcal O(\rm n)$，线性正比于原列表的规模。

查找

有序列表的查找算法如下：

template <typename T> //在有序列表内节点p（可能是trailer）的n个（真）前驱中，找到不大于e的最后者
ListNodePosi<T> List<T>::search ( T const& e, int n, ListNodePosi<T> p ) const {
// assert: 0 <= n <= rank(p) < _size
   do {
      p = p->pred; n--;  //从右向左
   } while ( ( -1 < n ) && ( e < p->data ) ); //逐个比较，直至命中或越界
   return p; //返回查找终止的位置
} //失败时，返回区间左边界的前驱（可能是header）——调用者可通过valid()判断成功与否

有序列表的查找算法与有序向量完全不同。这是因为尽管有序列表中的节点在逻辑上按照次序单调排列，但是这些节点的物理地址与逻辑次序毫无关系，故无法像有序向量那样应用减治策略（因为没办法快速确定分割点），从而不得不使用无序列表的顺序查找策略。

与无序列表的查找算法同理，该算法在最好的情况下运行时间为$\mathcal O(1)$，最坏情况下为$\mathcal O (\rm n)$。在等概率的前提下，平均运行时间也是$\mathcal O (\rm n)$。