DSA-5：查找算法之向量实现

上一篇文章中介绍了向量的一般接口，这些接口大部分是为无序向量设计的。而这篇文章要讨论的的查找算法全都是为有序向量设计的。可以看到，对有序向量而言，因为多包含了“有序性”这一重要信息，向量中某一元素的查找操作的效率可以提高很多。

二分查找

对于一个有序向量，以任一一个元素S[mi] = x为界，都可以将区间分为三个部分。并且由于向量是有序的，必然有：$\rm{S[lo, mi) \le S[mi] \le S(mi, hi)}$。于是，只需要将目标元$\rm e$与$\rm x$做一次比较，便可以视比较结果分为三种情况进一步处理：

1. 若$\rm e < x$，则若$\rm e$存在，那么它必属于左侧子区间$\rm S[lo, mi)$，故可深入其中继续查找
2. 若$\rm e > x$，则若$\rm e$存在，那么它必属于右侧子区间$\rm S(mi, hi)$，故也可深入其中继续查找
3. 若$\rm e = x$，那么就找到了目标元素，查找终止

下面的图片展示了这个算法的基本思路：

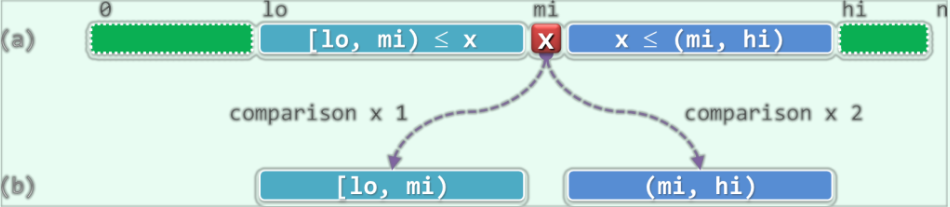
经过至多两次比较操作，我们要么已经找到了目标元素，要么可以将原问题简化为一个规模更小的同类的新问题。看到这里，你应当很自然地想到使用递归的方法了。接下来要介绍的几个查找算法的不同点仅在于切分点mi的策略，以及每次深入递归之前所做的比较操作的次数。

为了便于使用，现为向量类设计了一个统一的查找算法的接口。在这个接口中，它会随机地调用不同的查找算法的函数。

template <typename T> //在有序向量的区间[lo, hi)内，确定不大于e的最后一个节点的秩
Rank Vector<T>::search ( T const& e, Rank lo, Rank hi ) const { //assert: 0 <= lo < hi <= _size
   return ( rand() % 2 ) ? //按各50%的概率随机使用二分查找或Fibonacci查找
          binSearch ( _elem, e, lo, hi ) : fibSearch ( _elem, e, lo, hi );
}

二分查找（实现1）

实现

template <typename T> static Rank binSearch ( T* S, T const& e, Rank lo, Rank hi ) {
   while ( lo < hi ) { //每步迭代可能要做两次比较判断，有三个分支
      Rank mi = ( lo + hi ) >> 1; //以中点为轴点（区间宽度的折半，等效于宽度之数值表示的右移）
      if      ( e < S[mi] ) hi = mi; //深入前半段[lo, mi)继续查找
      else if ( S[mi] < e ) lo = mi + 1; //深入后半段(mi, hi)继续查找
      else                  return mi; //在mi处命中
   } //成功查找可以提前终止
   return -1; //查找失败
} //有多个命中元素时，不能保证返回秩最大者；查找失败时，简单地返回-1，而不能指示失败的位置

该算法以中点为界，将有序向量区间大致平均地分为前后两个子向量。另外，该算法使用了迭代的方法实现。（如果是以递归形式实现的话就是尾递归，可以改为迭代法实现。）

下图给出了上面的算法的一个实例，左边的子图为search(8, 0 ,7)右边的子图为search(3, 0, 7)。左子图查找成功，右子图查找失败。

复杂度

上面算法的实现策略可以概括为：以当前区间的居中元素作为目标元素的试探对象，因此每一步迭代之后无论沿着哪一个方向深入，新问题的规模都会减小一半。随着迭代的不断深入，目标查找区间的宽度以0.5的比例按几何级数的速度递减。于是经过至多$\log_2(\rm{hi - lo})$步迭代后，算法必然终止。又因为每一步迭代只需要常数时间，因此总体的时间复杂度为$\mathcal O(n)$。

查找长度

查找长度为查找算法中进行比较操作的次数。在查找算法中，每步迭代中的操作可以分为两种：元素的大小比较、秩的算数运算及其赋值。由于向量中存储的元素类型可能十分复杂，其比较操作可能会花费大量时间。因此在向量的查找算法中，元素的比较次数——也就是查找长素——是衡量算法性能的重要指标。

成功查找长度

对于长度为$\rm n$的向量，共有种$\rm n$可能的查找。这些查找的种类分别对应于某一个元素。实际上，每一种成功查找所对应的查找长度，仅对应于$\rm n$与目标元素的秩（该元素在向量中的位置），而与向量中元素的值无关。下面的图片给出了当$\rm n = 7$时向量各种情况下对应的查找长度。图中红色节点代表查找成功，紫色节点代表查找失败，每个节点中的数字表示该情况下的查找长度。

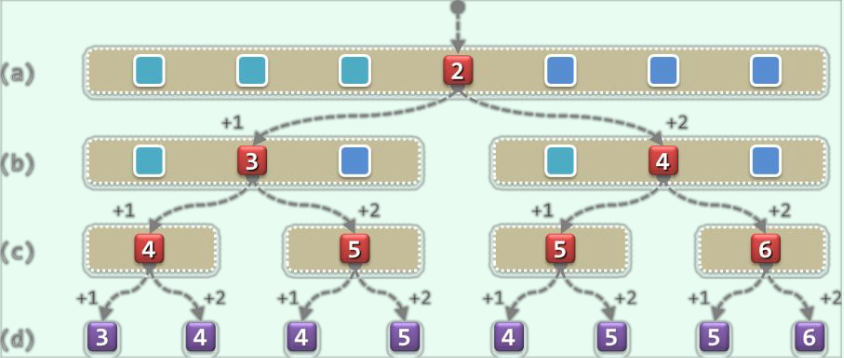
由图可知，假设待查找的目标元素等概率分布，平均成功查找长度为$(4 + 3 + 5 + 2 + 5 + 4 + 6) / 7 =4.14$。

为了估计出一般情况下的成功查找长度，仍在等概率条件下考察长度为$\rm{n = 2^k - 1}$的有序向量，所有元素对应的查找长素总和记为$\rm{C(k)}$，平均查找长度记为$c_{ave}$。

当$\rm k = 1$时，$\rm C(k) = 1$。当长度为$\rm 2^k - 1$时，有$\rm C(k) = [C(k - 1) + (2^{k-1} - 1)] + 2 + [C(k - 1) + 2(2^{k-1} - 1)] = 2C(k - 1) + 3\cdot 2^{k - 1} - 1$。

上面的公式中，左侧中括号内的$\rm C(k-1)$代表经过一次成功的比较（if(e < A[mi])）后，问题规模缩减为$\rm 2^{k - 1} - 1$。当向量规模为$\rm n = 2^k - 1$时，前缀中一共有$\rm 2^{k - 1} - 1$个元素。此时若目标元素在前缀中，那么无论在前缀中的哪个位置，他都已经经过一次比较了，之后要找到它至少也需要一次比较，这就是左侧中括号内$\rm 2^{k-1} - 1$的含义。

公式中，右侧中括号内的$\rm C(k-1)$代表经过一次失败的比较（if(e < A[mi])）与一次成功的比较（else if (A[mi < e])）后，问题规模缩减为$\rm 2^{k - 1} - 1$。当向量规模为$\rm n = 2^k - 1$时，后缀中一共有$\rm 2^{k - 1} - 1$个元素。此时若目标元素在后缀中，那么无论在后缀中的哪个位置，他都已经经过两次比较了，之后要找到它至少也需要两次比较，这就是左侧中括号内$\rm 2(2^{k-1} - 1)$的含义。

公式中的$2$很好理解，就是如果目标元素匹配了，就经过了两次失败的比较。

经过一系列的变换和推导，可以得出$\rm C(k) = (3k/2 - 1)\cdot (2^k - 1) + 3k/2$，进而得到$\rm c_{ave} = 3k/2 - 1 + 3k/(2\cdot (2^k - 1))$。

忽略$\rm c_{ave}$尾部的波动项，平均查找长度为$\mathcal O (1.5\rm{k}) = \mathcal O (1.5\cdot \log_2\rm n)$。

失败查找长度

失败查找长度不同于成功查找长度，只有在区间宽度缩减为0时，查找才失败。因此，失败查找的时间复杂度应该为$\Theta (logn)$。这里使用$\Theta$符号的原因是：失败查找的时间几乎是确定的，它不存在最坏和最好的情况，总是在$\log_2 n$附近。

不难发现，失败查找的可能情况总是比成功查找的可能情况多出一种。以上一小节给出的长度为7的向量为例，其失败查找长度为4.5。

仿照对平均成功查找长度的分析方法可以得出，一般情况下的平均失败查找长度也是$\mathcal O (1.5\cdot \log_2n)$。这里就不再分析了。

斐波那契查找

上述二分查找算法尽管在最坏情况下的效率可以达到$\mathcal O (logn)$，但是它还是存在着一些问题。以成功查找为例，即使是迭代（循环）次数相同的情况，各个元素对应的查找长度也不尽相同。这是因为在迭代中为了确定左右分支的方向，需要做1次到2次比较，从而造成不同情况下对应查找长度的不均衡，其中最短和最长分支所对应的查找长度相差约两倍。

为了解决上面的问题，有两种思路可以考虑：

1. 调整前、后区域的宽度，适当加长前子向量并缩短后子向量
2. 统一往两个方向深入所需要执行的比较次数

这里先考虑第一个解决思路。减而治之策略并不要求向量的切分点mi必须居中，在这里可以考虑按照黄金分割比例来确定mi。不妨假设向量的长度$\rm n = fib(k) - 1$，于是斐波那契查找算法可以用mi = fib(k - 1) - 1作为前、后子向量的切分点。这样一来，前后子向量的长度分别为$\rm fib(k - 1) - 1$与$\rm fib(k - 2) - 1 = (fib(k) - 1) - (fib(k - 1) - 1) - 1$。由此，无论朝哪个方向深入，新向量的长度从形式上都依然是某个斐波那契数减1，就像下图一样：

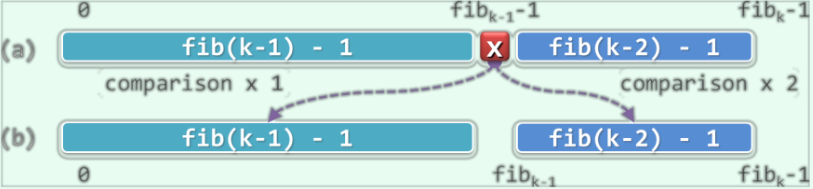
实现

#include "fibonacci/Fib.h" //引入Fib数列类
// Fibonacci查找算法（版本A）：在有序向量的区间[lo, hi)内查找元素e，0 <= lo <= hi <= _size
template <typename T> static Rank fibSearch ( T* S, T const& e, Rank lo, Rank hi ) {
    //用O(log_phi(n = hi - lo)时间创建Fib数列
   for ( Fib fib ( hi - lo ); lo < hi; ) {  //Fib数列制表备查；此后每步迭代仅一次比较、两个分支
      while ( hi - lo < fib.get() ) fib.prev(); //自后向前顺序查找（分摊O(1)）
      Rank mi = lo + fib.get() - 1; //确定形如Fib(k) - 1的轴点
      if      ( e < S[mi] ) hi = mi; //深入前半段[lo, mi)继续查找
      else if ( S[mi] < e ) lo = mi + 1; //深入后半段(mi, hi)继续查找
      else                  return mi; //在mi处命中
   } //成功查找可以提前终止
   return -1; //查找失败
} //有多个命中元素时，不能保证返回秩最大者；失败时，简单地返回-1，而不能指示失败的位置

斐波那契查找算法的主体框架与二分查找大致相同。主要区别在于使用黄金分割点取代中点作为切分点。为此需要借助Fib对象来获取斐波那契数列，这里获取的fib(hi - lo)为大小不小于向量中元素个数的斐波那契数。代码第6行的作用是根据fib(k)找到fib(k - 1)。如果hi - lo小于fib当前指向的值，则将fib前移一个，直到fib指向的值在$\rm [lo , hi)$之间。

性能分析

斐波那契查找倾向于适当加长需要1次比较方可确定的前端子向量，缩短需要2次比较方可以确定的后端子向量。通过这种方式来减小不同元素查找长度的差异。

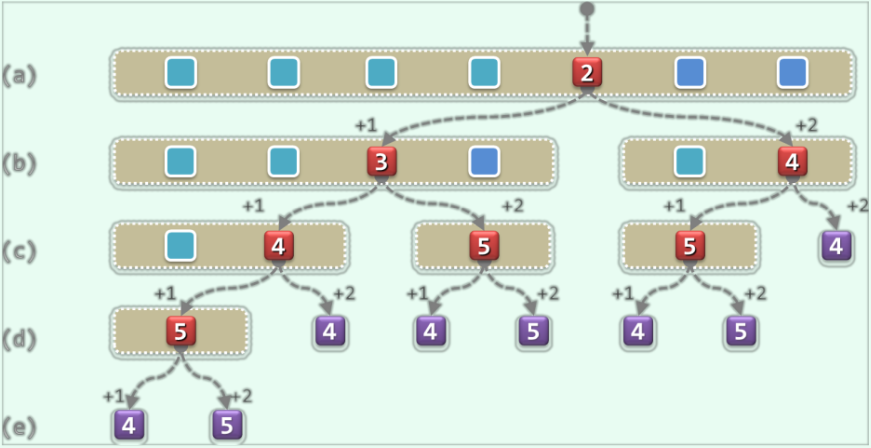
以上图为例，在假定各元素出现概率相等时，则平均成功查找长度为4，平均失败查找长度为4.38。相比于二分查找（实现1）中的平均查找长度的确有所改进。可以证明，斐波那契查找的平均查找长度为$\mathcal O (1.44\log_2n)$。

二分查找（实现2）

现在来讨论第二种缩小前后查找长度不均衡的策略：统一往两个方向深入所需要执行的比较次数。在这个版本的二分查找算法中，无论朝哪个方向的子向量深入查找，都只需要做1次元素的大小比较。具体过程如下图所示：

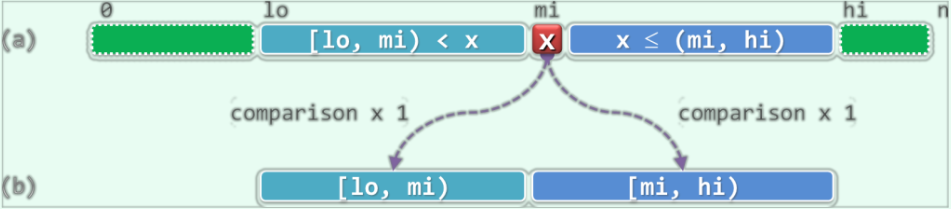
如图所示，该算法在每个切分点A[mi]处仅做一次比较。若目标元素小于A[mi]，则深入前端子向量A[lo, mi)中继续查找；否则深入后端子向量A[mi, hi)中继续查找。

实现

// 二分查找算法（版本B）：在有序向量的区间[lo, hi)内查找元素e，0 <= lo < hi <= _size
template <typename T> static Rank binSearch ( T* S, T const& e, Rank lo, Rank hi ) {
   while ( 1 < hi - lo ) { //每步迭代仅需做一次比较判断，有两个分支；成功查找不能提前终止
      Rank mi = ( lo + hi ) >> 1; //以中点为轴点（区间宽度的折半，等效于宽度之数值表示的右移）
      ( e < S[mi] ) ? hi = mi : lo = mi; //经比较后确定深入[lo, mi)或[mi, hi)
   } //出口时hi = lo + 1，查找区间仅含一个元素A[lo]
   return e < S[lo] ? lo - 1 : lo; //返回位置，总是不超过e的最大者
} //有多个命中元素时，返回秩最大者；查找失败时，简单地返回-1，而不能指示失败的位置

该版本的二分查找算法只有等到区间的宽度缩小为1（只剩最后一个元素）时迭代才会终止。哪怕在第一步迭代中就已经匹配到了目标元素，也得继续进行迭代，调整区间端点，直到区间中只剩一个元素。最后，再对这剩下的最后一个元素进行一次比较来判断查找是否成功。

性能分析

显然，该算法的渐进复杂度为$\mathcal O (logn)$。由于无论如何只有在区间中只有一个元素时迭代才会停止，因此最好情况下的效率会有所倒退。但是作为补偿，最坏情况下的效率也会有所提高（最长的查找长度相比于“实现1”中缩短1倍）。无论是成功查找还是失败查找，该版本的二分查找算法中各分支的查找长度都更加接近，故整体性能更加稳定。

二分查找（实现3）

二分查找（实现2）仍有可以改进之处：比如它在返回匹配成功的元素时，若有重复的多个匹配元素，它只能在这些元素中“随机”地报告其中一个（并不是真的随机，这个跟mi的选取方法有关）；此外，在查找失败的时候，该算法也只能简单地返回一个-1。

对二分查找（实现2）的代码进行一些改进便可改进上述缺点。

实现

// 二分查找算法（版本C）：在有序向量的区间[lo, hi)内查找元素e，0 <= lo <= hi <= _size
template <typename T> static Rank binSearch ( T* S, T const& e, Rank lo, Rank hi ) {
   while ( lo < hi ) { //每步迭代仅需做一次比较判断，有两个分支
      Rank mi = ( lo + hi ) >> 1; //以中点为轴点（区间宽度的折半，等效于宽度之数值表示的右移）
      ( e < S[mi] ) ? hi = mi : lo = mi + 1; //经比较后确定深入[lo, mi)或(mi, hi)
   } //成功查找不能提前终止
   return lo - 1; //循环结束时，lo为大于e的元素的最小秩，故lo - 1即不大于e的元素的最大秩
} //有多个命中元素时，返回秩最大者；查找失败时，能够返回失败的位置

这个版本的二分查找算法是在当区间的长度缩减为0时才停止迭代，此外在每次转入后端分支时，子向量的左边界取作mi + 1而不是mi。这样做的理由是：**$\rm A[0, lo)$中的元素小于等于$\rm e$，$\rm A[hi, n)$中的元素均大于$\rm e$**。使用数学归纳法可以证明该命题。

首次迭代时，lo = 0，hi = n，因此$\rm A[0, lo)$与$\rm A[hi, n)$均为空，命题成立。

考察在某次迭代中的情况。如果$\rm e < A[mi]$，则令hi = mi，这使得$\rm A[hi, n)$向左扩展，该区间内的元素仍然都大于$\rm e$。如果$\rm e \ge A[mi]$，则令lo = mi + 1，这使得$\rm A[0, lo)$向右扩展，该区间内的元素仍然小于等于$\rm e$。在循环终止时有lo = hi，考察A[lo - 1]和A[lo]：作为$\rm A[0, lo)$中的最后一个元素，A[lo - 1]必然不大于$\rm e$；作为$\rm A[hi, n)$中的第一个元素，A[lo]一定大于$\rm e$。所以此时A[lo - 1]就是原向量中不大于$\rm e$的最后一个元素，因此算法只用返回lo - 1。

下面的图片解释了该算法的思路：

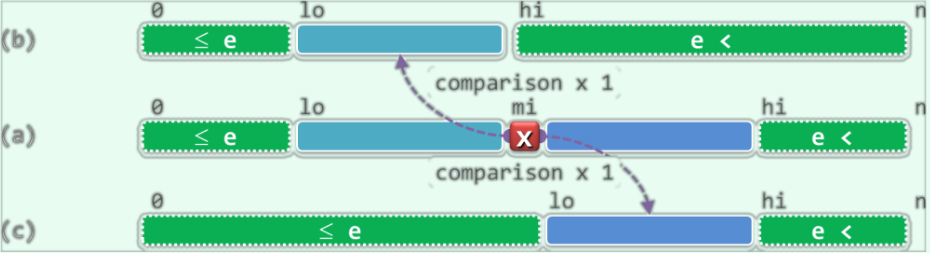
可见，这个版本的二分查找算法在查找成功时，（若有多个匹配元素）会返回众多匹配元素的最后一个；在查找失败时，会返回向量中小于目标元素的各元素中的最大者。