DSA-1：算法的基本概念与复杂度分析

关于算法的基本概念

定义

算法是基于特定的计算机模型，旨在解决某一信息处理问题而设计的一个指令序列。

基本特性

输入与输出

任何算法都需要通过输入来获得某一问题的实例，并且通过输出来给出问题的解。

基本操作、确定性与可行性

• 基本操作：可以理解为计算机可以执行的，汇编语言中的一条命令，如MOV、SUB等
• 确定性与可行性：算法可以描述为由若干语义明确的基本操作组成的指令序列，且每一基本操作在对应的计算模型中均可兑现

有穷性与正确性

• 有穷性：算法在执行有限次基本操作之后会终止并且输出
• 正确性：算法给出的输出是正确的

如何证明算法的有穷性与正确性

• 问题的有效规模：其定义由问题的具体形式决定，如算法中需要操作的元素个数、需要操作的bit位等
• 算法的单调性：问题的有效规模会随着算法的推进而递减
• 算法的不变性：算法在任何时候都满足问题的前提条件，并且当问题的有效规模缩减到0时依旧满足，此时不变性等价于正确性
• 证明算法有穷性和正确性的一个重要技巧就是从适当的角度审视整个计算过程，找到其中所具有的某种不变性和单调性

退化性和鲁棒性

• 退化性：算法可以处理各种极端的输入个例（退化情况）
• 鲁棒性：算法能够尽可能充分应对极端输入的情况

重用性

算法的总体框架可以便捷地推广到其他应用场合。

算法的效率问题

• 可计算性：算法应当是在有限时间内能给出结果的，应当是必然终止的，也即满足有穷性
• 难解性：算法满足有穷性但是花费的时间成本太高，这样的算法是难解的

算法的复杂度度量

时间复杂度

时间复杂度简介

算法的时间复杂度衡量了算法在处理不同规模问题时所需要的时间长短，它是算法执行时间的变化趋势随输入规模变化的一个函数。

对特定算法，其处理问题所需要的时间可以记为$T(n)$。表达式中的$n$即为问题的输入规模，比如对含有$n$个元素的向量进行排序，需要$T(n)$时间。

另外需要注意的是，从保守估计的角度出发，在多个不同的规模为$n$的输入中，$n$为算法执行时间$T(n)$最长的所对应的那个输入的规模，并且以此时的$T(n)$来衡量算法的时间复杂度。

渐进复杂度

渐进复杂度用于考察算法在处理大规模问题时的能力好坏，它注重复杂度的总体变化趋势和增长速度。因此，在衡量算法的复杂度时，其问题规模$n$通常很大。

大$\mathcal O$记号

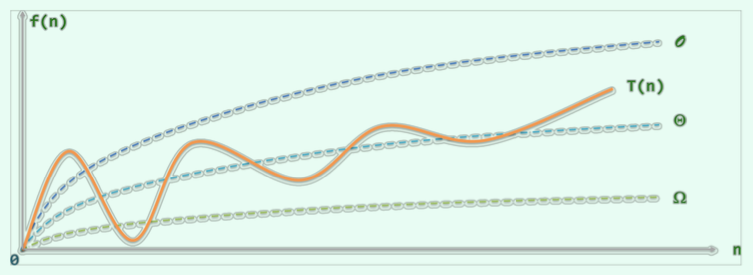
出于保守估计，我们一般关心$T(n)$的渐进上界，以“大$\mathcal{O}$记号”表示：$\mathcal{O}(n)$。该记号在未来分析算法的复杂度时最为常用。

关于其定义，有：$T(n)\le c\cdot f(n) $，即认为在$n$足够大以后，$f(n)$给出了$T(n)$增长速度的一个渐进上界。此时记$T(n) = \mathcal O (f(n))$。这里可以将$c$理解为执行基本操作所需要的时间，$f(n)$为对规模为$n$的输入，需要的操作次数。

大$\mathcal O$记号有以下性质：

• 对任一常数$c\gt 0$，有$\mathcal O (f(n)) = \mathcal O (c\cdot f(n))$
• 对任意常数$a\gt b\gt 0$，有$\mathcal O (n^a + n^b) = \mathcal O (n^a)$

对于上面的性质，可以理解为：**$c$与$n^b$等项都可以通过$n^a$的形式表示**。

由于在不同的操作系统上，算法中的指令的执行时间不尽相同，因此将$T(n)$定义为算法所执行的基本操作的总次数比较合适。这里的基本操作，在不同的算法下有着不同的内容。

以起泡排序为例，在每一轮内循环中，需要扫描和比较$n-1$对元素，至多需要交换$n-1$对元素，这里的比较和交换都属于基本操作；外循环最多执行$n-1$次，因此总共需要执行的基本操作不会超过$2(n-1)^2$次，有：$T(n) = \mathcal O (2(n-1)^2)= \mathcal O (n^2)$。

上面的分析意味着，起泡排序在最坏的情况下，其运行时间不会超过$\mathcal O (n^2)$。

void bubblesort1A ( int A[], int n ) { //起泡排序算法（版本1A）：0 <= n
    bool sorted = false; //整体排序标志，首先假定尚未排序
    while ( !sorted ) { //在尚未确认已全局排序之前，逐趟进行扫描交换
       sorted = true; //假定已经排序
       for ( int i = 1; i < n; i++ ) { //自左向右逐对检查当前范围A[0, n)内的各相邻元素
          if ( A[i - 1] > A[i] ) { //一旦A[i - 1]与A[i]逆序，则
             swap ( A[i - 1], A[i] ); //交换之，并
             sorted = false; //因整体排序不能保证，需要清除排序标志
          }
       }
       n--; //至此末元素必然就位，故可以缩短待排序序列的有效长度
    }
 } //借助布尔型标志位sorted，可及时提前退出，而不致总是蛮力地做n - 1趟扫描交换

大$\Omega$记号

大$\Omega$记号给出了对算法在最好情况下的复杂度，其定义为：若$T(n)\ge c\cdot g(n)$，则认为在$n$足够大之后，$g(n)$给出了$T(n)$的一个渐进下界。此时记$T(n)=\Omega (g(n))$。

对于上面给出的起泡排序算法，假设问题的输入为一个长度为$n$的已经完全排序完成的向量，那么该算法仍然需要进行$n-1$次比较来确定排序已经完成，因此其最好渐进时间复杂度为$\Omega (n)$。

大$\Theta$记号

大$\Theta$记号表示的算法复杂度介于大$\mathcal O$和大$\Omega$之间，其定义为：若$c_1\cdot h(n)\le T(n) \le c_2 \cdot h(n)$，则认为在$n$足够大之后，$h(n)$给出了$T(n)$的一个确界。此时记$T(n) = \Theta(h(n))$。

$\Theta (n)$给出了对算法复杂度的准确估计，算法在实际中的运行时间与其同阶。

空间复杂度

空间复杂度衡量了算法所需存储空间（内存）的多少，以上用于衡量时间复杂度的几种渐进记号同样适用于衡量空间复杂度。

对于空间复杂度，一般不算入原始输入本身所占用的空间，只考虑在算法运行过程中需要的空间。此外，一般在评估算法性能时，我们不必考虑空间复杂度。因为就渐进复杂度的意义来说，任一算法的任何一次运行过程中所消耗的存储空间，都不可能超过其执行基本操作的累积次数。时间复杂度本身就是空间复杂度的一个天然上界。

几种典型的复杂度层次

常数$\mathcal O (1)$

在任何情况下，算法仅含有一次或者常数次基本操作，运行时间都为固定的常数，与算法的输入规模无关。这种算法被称为“常数时间复杂度算法”。

对于仅需要$\mathcal O (1)$辅助空间的算法，称为“就地算法”。

对数$\mathcal O (logn)$

对数复杂度层次常常出现在每进行一次循环问题的规模就减半的情况下，此时对数的底数为2。一般情况下不会专门给出对数的底数，而只是将其笼统得记为$logn$的形式。

显然，具有对数复杂度的算法肯定包含循环，循环的次数受到问题输入规模的影响，约等于$logn$。在循环之外，算法当然可能包括其他常数次基本操作，但是算法的执行时间还是主要由循环的次数决定。

更一般的，凡是运行时间可以表示和度量为$T(n) = \mathcal O (log^c n)$（$c$为正的常数）的算法，均统称为“对数多项式时间复杂度的算法”。此类算法的效率相对来说也是比较高效的。

线性$\mathcal O (n)$

线性复杂度的算法同样相当常见。比如求n个数的和——对于大多数其他问题亦是如此——需要对输入的每个单元至少访问一次，因此至少需要n轮循环。该算法的运行时间随问题的输入规模增大而线性增大，其效率也还算令人满意。

多项式$\mathcal O (poly(n))$

该类算法的运行时间可以表示为问题输入规模$n$的多项式形式，如前面提到的起泡排序算法，其复杂度为$\mathcal O (n^2)$。无论多项式中$n$的最高次幂为多少，只要复杂度符合这种形式的算法都可以归入此类，尽管在考虑幂次后他们的复杂度会有天壤之别。

在实际应用中，具有该复杂度的算法通常是可以忍受的。如果一个问题存在一个复杂度在此范围之内的算法，那么这个问题被称为是可以有效求解的或者易解的，否则称为难解的。

指数$\mathcal O (2^n)$

凡是运行时间可以表示和度量为$T(n) = \mathcal O (a^n)$ （$a\gt 1$）形式的算法，均属于指数时间复杂度算法。比如，对于“求一个含有n个元素的集合的所有子集”的问题，它含有$2^n$个子集，因此其复杂度为指数的。

通常认为，指数复杂度的算法无法真正用于实际问题之中。

关于输入规模的额外讨论

考察下面的例子：

__int64 power2BF_I ( int n ) { //幂函数2^n算法（蛮力迭代版），n >= 0
   __int64 pow = 1; //O(1)：累积器初始化为2^0
   while ( 0 < n -- ) //O(n)：迭代n轮，每轮都
      pow <<= 1; //O(1)：将累积器翻倍
   return pow; //O(1)：返回累积器
} //O(n) = O(2^r)，r为输入指数n的比特位数

该算法的功能是在不超过一位的移位运算下对任意非负整数n，计算$2^n$。一般我们将该算法的时间复杂度认为是$\mathcal O (n)$的，但是如果将输入n的二进制位数$r = 1 + \lfloor log_2 n\rfloor$作为输入规模去考虑的话，则其运行时间为$2^r$。

从上面的例子可知，对于算法复杂度的界定，都是相对于问题的输入规模而言的。因此对同一个算法，可能得到不同的复杂度分析的结论。严格来说，待计算问题的输入规模应定义为“用于描述输入所需要的空间规模”，也即问题输入所占的内存空间（个人理解这样定义的原因是计算机的基本操作都是基于二进制位进行的）。

以输入的自然独立体个数n的数值（如待排序元素的个数、待求和的元素个数等）作为基准得出的$\mathcal O (logn)$与$\mathcal O (n)$复杂度，被分别称为伪对数的和伪线性的复杂度。但是一般情况下，我们还是以输入的自然独立体个数n的数值作为分析算法复杂度的基准。